PMT function in Excel

The PMT function in Excel calculates the payment for a loan based on constant payments and a constant interest rate. This page contains many easy to follow PMT examples.

PMT examples

Consider a loan with an annual interest rate of 6%, a 20-year duration, a present value of $150,000 (amount borrowed) and a future value of 0 (that's what you hope to achieve when you pay off a loan).

1. The PMT function below calculates the annual payment.

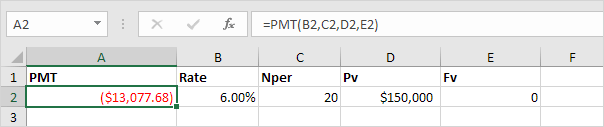
Note: if the fifth argument is omitted, it is assumed that payments are due at the end of the period. We pay off a loan of $150,000 (positive, we received that amount) and we make annual payments of $13,077.68 (negative, we pay).

2. The PMT function below calculates the quarterly payment.

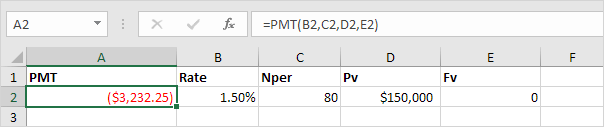
Note: we make quarterly payments, so we use 6%/4 = 1.5% for Rate and 20*4 = 80 for Nper (total number of periods).

3. The PMT function below calculates the monthly payment.

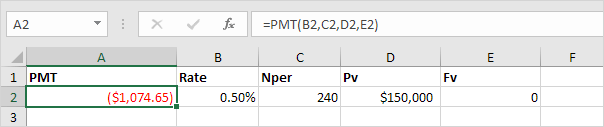
Note: we make monthly payments, so we use 6%/12 = 0.5% for Rate and 20*12 = 240 for Nper (total number of periods).

Consider an investment with an annual interest rate of 8% and a present value of 0. How much money should you deposit at the end of each year to have $1,448.66 in the account in 10 years?

4. The PMT function below calculates the annual deposit.

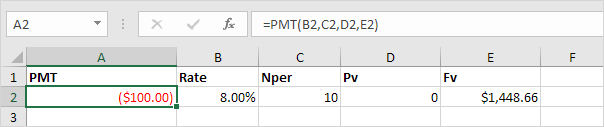
Explanation: in 10 years time, you pay 10 * $100 (negative) = $1000, and you'll receive $1,448.66 (positive) after 10 years. The higher the interest, the faster your money grows.

Consider an annuity with an annual interest rate of 6% and a present value of $83,748.46 (purchase value). How much money can you withdraw at the end of each month for the next 20 years?

5. The PMT function below calculates the monthly withdrawal.

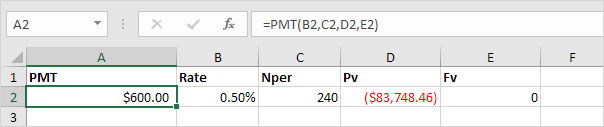
Explanation: you need a one-time payment of $83,748.46 (negative) to pay this annuity. You'll receive 240 * $600 (positive) = $144,000 in the future. This is another example that money grows over time.

PPMT and IPMT

Consider a loan with an annual interest rate of 5%, a 2-year duration and a present value (amount borrowed) of $20,000.

1. The PMT function below calculates the monthly payment.

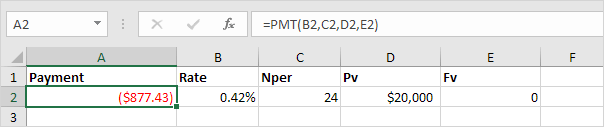
Note: we make monthly payments, so we use 5%/12 for Rate and 2*12 for Nper (total number of periods).

2. The PPMT function in Excel calculates the principal part of the payment. The second argument specifies the payment number.

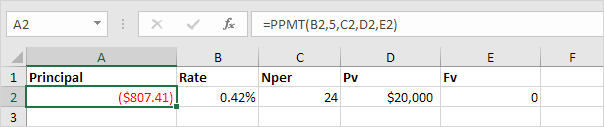
Explanation: the PPMT function above calculates the principal part of the 5th payment.

3. The IPMT function in Excel calculates the interest part of the payment. The second argument specifies the payment number.

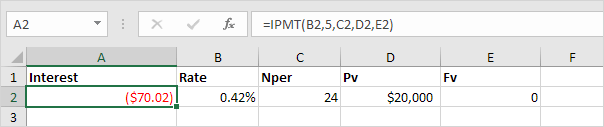
Explanation: the IPMT function above calculates the interest part of the 5th payment.

4. It takes 24 months to pay off this loan. Create a loan amortization schedule (see picture below) to clearly see how the principal part increases and the interest part decreases with each payment.

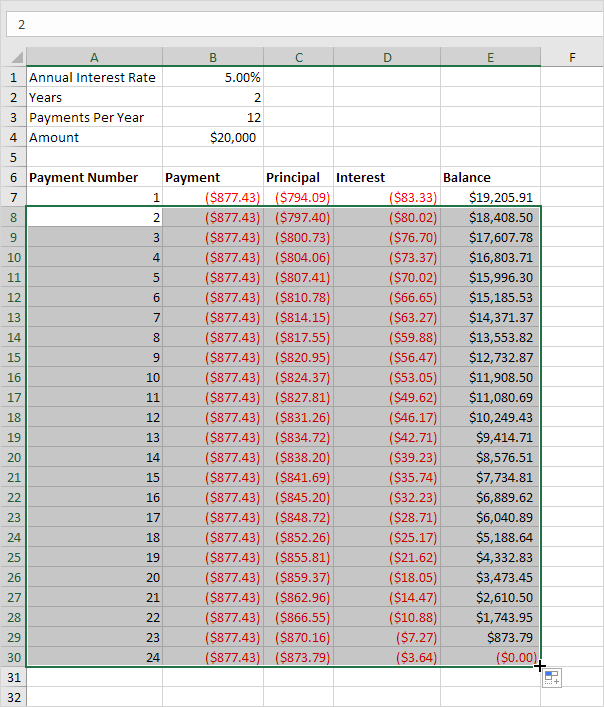
Note: the principal part and the interest part always add up to the payment amount.

If you're new here, welcome to Excel Easy! Join over 1 million monthly Excel learners. You can find popular courses here: Excel Functions and Data Analysis in Excel.