Correlation Analysis in Excel

The correlation coefficient (a value between -1 and +1) tells you how strongly two variables are related to each other. We can use the CORREL function or the Analysis Toolpak add-in in Excel to find the correlation coefficient between two variables.

- A correlation coefficient of +1 indicates a perfect positive correlation. As variable X increases, variable Y increases. As variable X decreases, variable Y decreases.

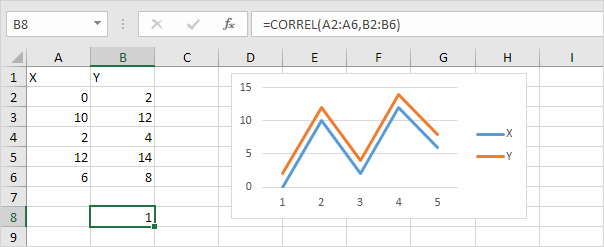
- A correlation coefficient of -1 indicates a perfect negative correlation. As variable X increases, variable Z decreases. As variable X decreases, variable Z increases.

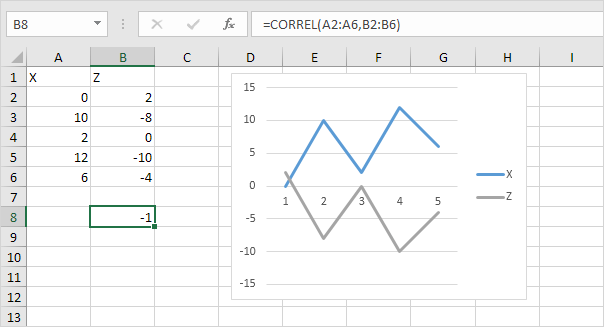
- A correlation coefficient near 0 indicates no correlation.

To use the Analysis Toolpak add-in in Excel to quickly generate correlation coefficients between multiple variables, execute the following steps.

1. On the Data tab, in the Analysis group, click Data Analysis.

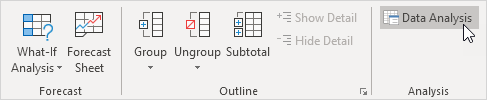
Note: can't find the Data Analysis button? Click here to load the Analysis ToolPak add-in.

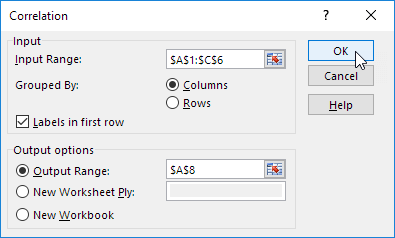
2. Select Correlation and click OK.

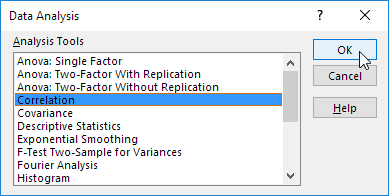
3. For example, select the range A1:C6 as the Input Range.

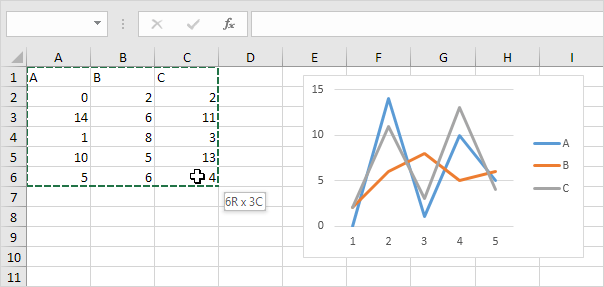
4. Check Labels in first row.

5. Select cell A8 as the Output Range.

6. Click OK.

Result:

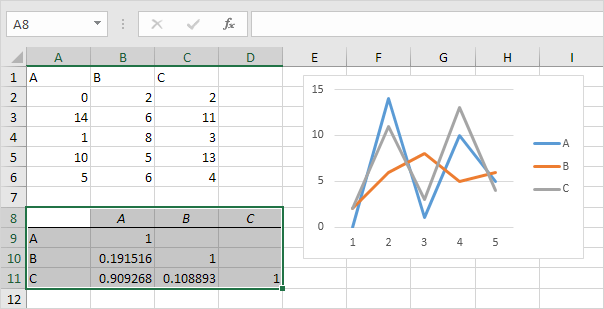
Conclusion: variables A and C are positively correlated (0.91). Variables A and B are not correlated (0.19). Variables B and C are also not correlated (0.11). You can verify these conclusions by looking at the graph.

If you're new here, welcome to Excel Easy! Join over 1 million monthly Excel learners. You can find popular courses here: Excel Functions and Data Analysis in Excel.