Financial Functions in Excel

To illustrate Excel's most popular financial functions, we consider a loan with monthly payments, an annual interest rate of 6%, a 20-year duration, a present value of $150,000 (amount borrowed) and a future value of 0 (that's what you hope to achieve when you pay off a loan).

We make monthly payments, so we use 6%/12 = 0.5% for Rate and 20*12 = 240 for Nper (total number of periods). If we make annual payments on the same loan, we use 6% for Rate and 20 for Nper.

PMT

Select cell A2 and insert the PMT function.

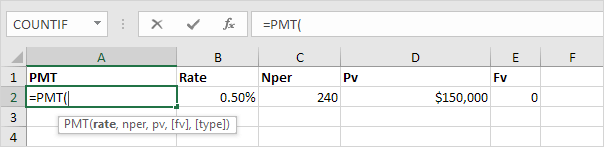
Note: the last two arguments are optional. For loans, Fv can be omitted (the future value of a loan equals 0, however, it's included here for clarification). If Type is omitted, it is assumed that payments are due at the end of the period.

Result: the monthly payment equals $1,074.65.

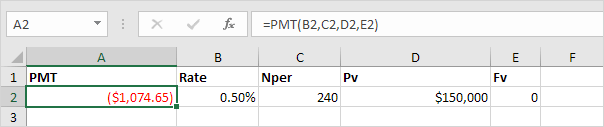
Tip: when working with financial functions in Excel, always ask yourself the question, am I making a payment (negative) or am I receiving money (positive)? We pay off a loan of $150,000 (positive, we received that amount) and we make monthly payments of $1,074.65 (negative, we pay). Visit our page about the PMT function for many more examples.

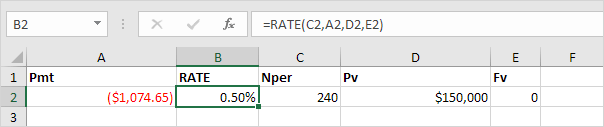
RATE

If Rate is the only unknown variable, we can use the RATE function to calculate the interest rate.

NPER

Or the NPER function. If we make monthly payments of $1,074.65 on a 20-year loan, with an annual interest rate of 6%, it takes 240 months to pay off this loan.

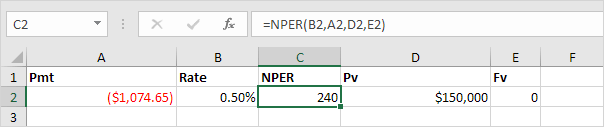
We already knew this, but we can change the monthly payment now to see how this affects the total number of periods.

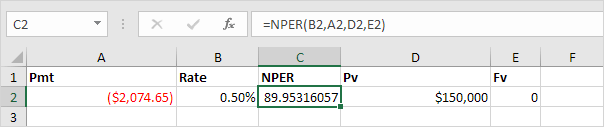
Conclusion: if we make monthly payments of $2,074.65, it takes less than 90 months to pay off this loan.

PV

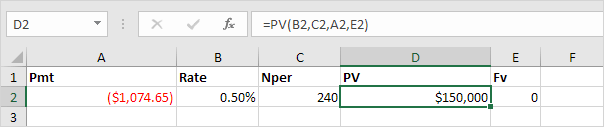
Or the PV (Present Value) function. If we make monthly payments of $1,074.65 on a 20-year loan, with an annual interest rate of 6%, how much can we borrow? You already know the answer.

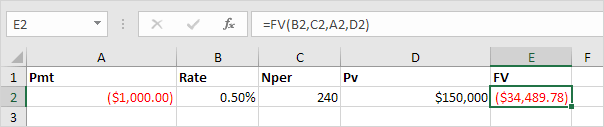
FV

And we finish this chapter with the FV (Future Value) function. If we make monthly payments of $1,074.65 on a 20-year loan, with an annual interest rate of 6%, do we pay off this loan? Yes.

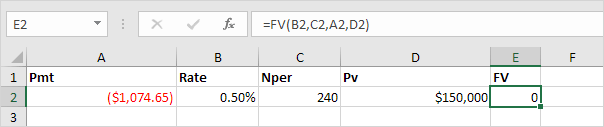
But, if we make monthly payments of only $1,000.00, we still have debt after 20 years.

If you're new here, welcome to Excel Easy! Join over 1 million monthly Excel learners. You can find popular courses here: Excel Functions and Data Analysis in Excel.