Investment or Annuity
This example teaches you how to calculate the future value of an investment or the present value of an annuity.
Tip: when working with financial functions in Excel, always ask yourself the question, am I making a payment (negative) or am I receiving money (positive)?
Investment
Assume that at the end of every year, you deposit $100 into a savings account. At an annual interest rate of 8%, how much will your investment be worth after 10 years?
1. Insert the FV (Future Value) function.
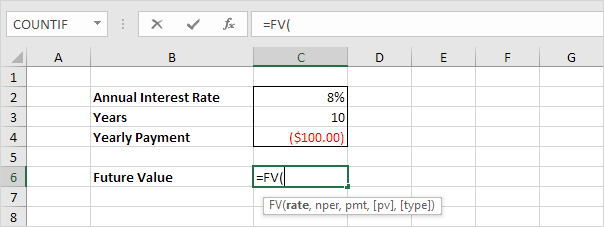
2. Enter the arguments.
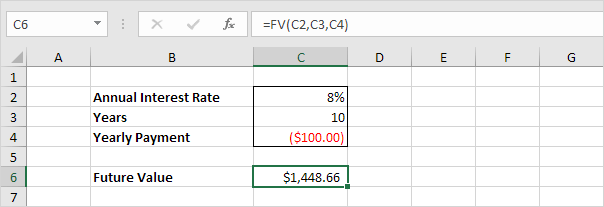
In 10 years time, you pay 10 * $100 (negative) = $1000, and you'll receive $1,448.66 (positive) after 10 years. The higher the interest, the faster your money grows.
Note: the last two arguments are optional. If omitted, Pv = 0 (no present value). If Type is omitted, it is assumed that payments are due at the end of the period.
Annuity
Assume you want to purchase an annuity that will pay $600 a month, for the next 20 years. At an annual interest rate of 6%, how much does the annuity cost?
1. Insert the PV (Present Value) function.
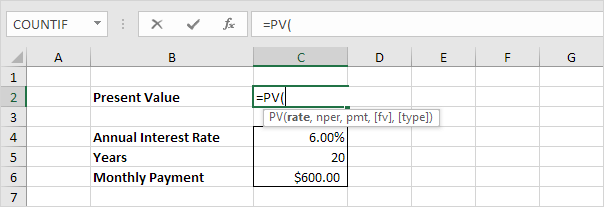
2. Enter the arguments.
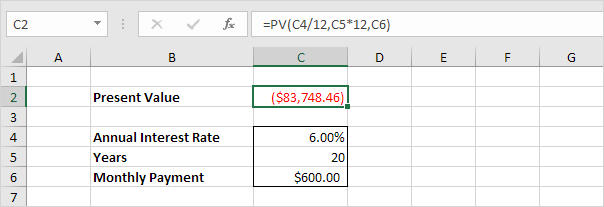
You need a one-time payment of $83,748.46 (negative) to pay this annuity. You'll receive 240 * $600 (positive) = $144,000 in the future. This is another example that money grows over time.
Note: we receive monthly payments, so we use 6%/12 = 0.5% for Rate and 20*12 = 240 for Nper. The last two arguments are optional. If omitted, Fv = 0 (no future value). If Type is omitted, it is assumed that payments are due at the end of the period. This annuity does not take into account life expectancy, inflation etc.